Understanding HASHING

The mapping between an item and the slot where that item belongs in the hash table is called the hash function.

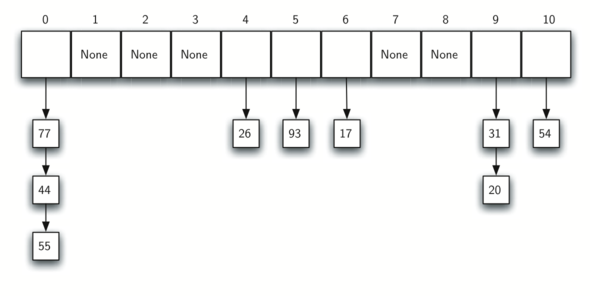
Once the hash values have been computed, we can insert each item into the hash table at the designated position. Note that 6 of the 11 slots are now occupied. This is referred to as the load factor, and is commonly denoted by load-factor=number_of_items/table_size.

According to the hash function, two or more items would need to be in the same slot. This is referred to as a collision (it may also be called a clash).

Given a collection of items, a hash function that maps each item into a unique slot is referred to as a perfect hash function.

Unfortunately, given an arbitrary collection of items, there is no systematic way to construct a perfect hash function.

One way to always have a perfect hash function is to increase the size of the hash table so that each possible value in the item range can be accommodated. This guarantees that each item will have a unique slot.

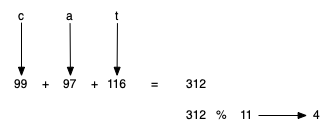
Get a hash for a string

Collision Resolution

When two items hash to the same slot, we must have a systematic method for placing the second item in the hash table. This process is called collision resolution. As we stated earlier, if the hash function is perfect, collisions will never occur. However, since this is often not possible, collision resolution becomes a very important part of hashing.

One method for resolving collisions looks into the hash table and tries to find another open slot to hold the item that caused the collision.

A simple way to do this is to start at the original hash value position and then move in a sequential manner through the slots until we encounter the first slot that is empty. Note that we may need to go back to the first slot (circularly) to cover the entire hash table. This collision resolution process is referred to as open addressing in that it tries to find the next open slot or address in the hash table. By systematically visiting each slot one at a time, we are performing an open addressing technique called linear probing.

A disadvantage to linear probing is the tendency for clustering; items become clustered in the table. This means that if many collisions occur at the same hash value, a number of surrounding slots will be filled by the linear probing resolution.

The general name for this process of looking for another slot after a collision is rehashing. With simple linear probing, the rehash function is new_hash=rehash(old_hash) where rehash(pos)=(pos+1)%size, or rehash(pos)=(pos+3)%size. In general, rehash(pos)=(pos+skip)%size. It is important to note that the size of the skip must be such that all the slots in the table will eventually be visited. Otherwise, part of the table will be unused. To ensure this, it is often suggested that the table size be a prime number.

An alternative method for handling the collision problem is to allow each slot to hold a reference to a collection (or chain) of items. Chaining allows many items to exist at the same location in the hash table. When collisions happen, the item is still placed in the proper slot of the hash table.